Symmetry Operations and Bravis Lattices

Symmetry operations and Bravis lattices are fundamental concepts in crystallography and solid-state physics. Symmetry operations describe the ways in which a crystal structure can be transformed while maintaining its overall appearance, and Bravis lattices define the periodic arrangement of lattice points in a crystal. Here, I'll provide an overview of these concepts with equations where appropriate.

Symmetry Operations

Symmetry operations are transformations that leave a crystal's appearance unchanged. They include:

1. Translation (T)

This operation involves moving all points in the crystal by a certain vector without changing their relative positions. The equation for a translation is:

RT​(x,y,z)=(x+a,y+b,z+c)

    Where \((a, b, c)\) is the translation vector.

2. Rotation (R)

 A rotation operation involves rotating the crystal around an axis passing through a point. The equation for a rotation is more complex and typically involves matrix multiplication.

3. Reflection (σ)

 A reflection operation mirrors the crystal across a plane. For a reflection across the xy-plane, the equation is:

Rσ​(x,y,z)=(x,y,−z)

   Similar equations can be written for reflections across other planes.

4. Inversion (i)

Inversion is a central point symmetry operation, which transforms each point to its opposite across a central point. The equation for inversion is

Ri​(x,y,z)=(−x,−y,−z)

5. Improper Rotation (S)

 An improper rotation operation combines a rotation with a reflection. It can be described using equations similar to those for rotations and reflections.

Bravis Lattices

Bravis lattices define the repeating, three-dimensional arrangement of lattice points in a crystal. There are 14 possible Bravis lattices, which can be categorized into seven crystal systems: 

• Triclinic
• Monoclinic
• Orthorhombic 
• Tetragonal
• Rhombohedral (trigonal) 
• Hexagonal
• Cubic

The equations for these lattice types are based on the lattice vectors ((a, b, c)) and lattice constants \(a, b, c, \alpha, \beta, \gamma\), which describe the size and shape of the unit cell.

Here are the equations for some common Bravis lattices:

Bravis Lattices

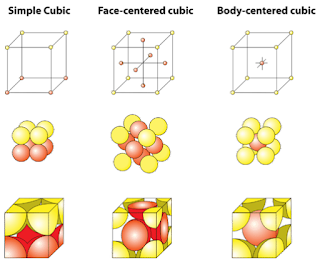
1. Simple Cubic (SC)

    Lattice Points: 1

    Equations:

     (a = b = c)

α=β=γ=90∘

2. Body-Centered Cubic (BCC)

   Lattice Points: 2

    Equations:

     (a = b = c)

α=β=γ=90∘

3. Face-Centered Cubic (FCC)

    Lattice Points: 4

    Equations:

     (a = b = c)

α=β=γ=90∘

These equations describe the unit cell parameters and symmetry operations associated with each Bravis lattice. They are essential in characterizing and understanding the structure of crystalline materials.